개발기록장

트리

4 min read

용어 정의

트리 : 나무 기둥에서 가지가 뻗어나가는 모습을 거꾸로 뒤집어 놓은 모양. 따라서 나무 밑둥 (루트)이 맨 위에 있음

노드 : 트리를 구성하는 요소. 맨 위에 있는 노드를 루트라고 함

엣지 : 노드와 노드를 연결하는 선. 간선이라고도 함

레벨 : 루트 노드로부터 특정 노드까지 거쳐가는 최소한의 간선 수

부모 노드 : 기준 노드 위에 있는 노드
자식 노드 : 기준 노드 하위에 있는 노드
형제 노드 : 같은 부모를 가지는 노드
리프 노드 : 자식이 없는 노드. 말단 노드라고도 함

구현 예시

배열로 표현

  • 이진 트리의 경우 가능한 방식.
  • 트리를 0번 인덱스가 아닌 1번 인덱스부터 넣는다고 가정할 때 아래의 공식이 작용함
  • 왼쪽 자식 노드의 인덱스는 부모 노드의 배열 인덱스 * 2
  • 오른쪽 자식 노드의 인덱스는 부모 노드의 배열 인덱스 * 2 + 1

포인터로 표현

  • 왼쪽 자식 노드 포인터 / 값 / 오른쪽 자식 노드 포인터
  • 구현 난이도 어려움

인접 리스트로 표현

  • 바로 한 단계 자식 노드를 저장함

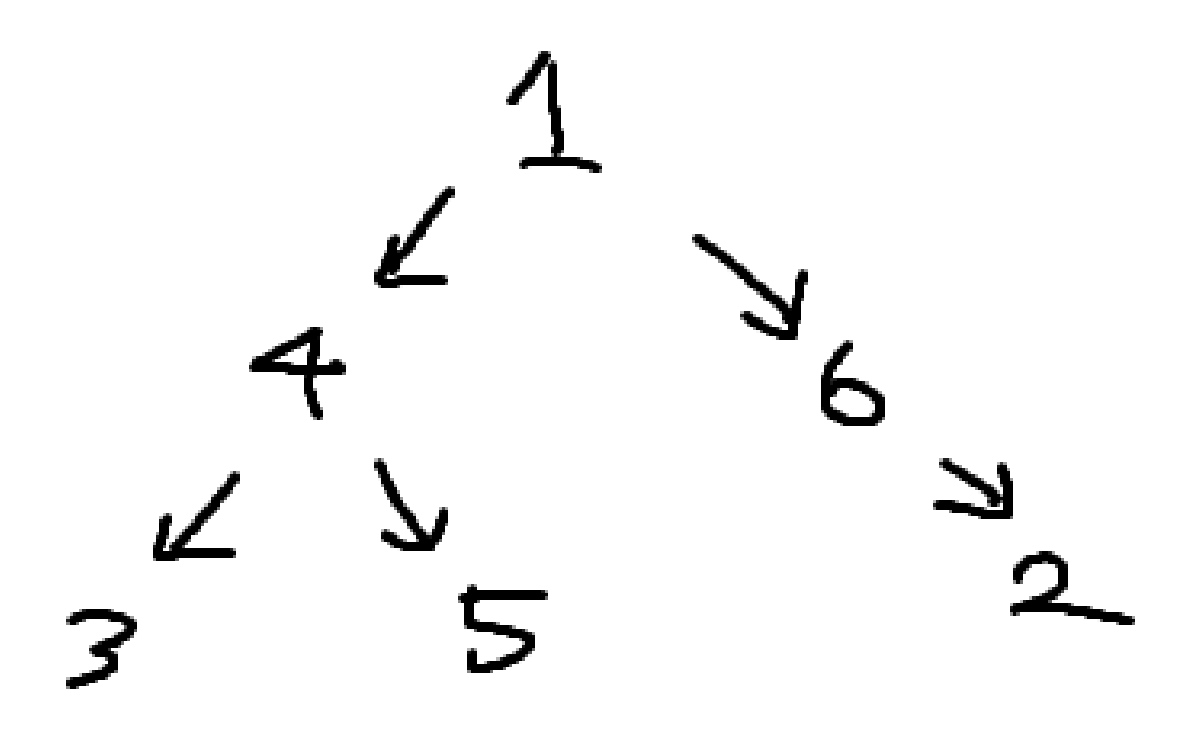
  • 이 그래프를 인접 리스트로 표현하면 아래와 같음
1 -> 4, 6
2
3
4 -> 3, 5
5
6 -> 2

순회 방법

전위 순회

  • 부모 → 왼쪽 자식 → 오른쪽 자식
  • 거치는 노드를 우선 방문함
  • 트리를 복사할 때 많이 사용됨

중위 순회

  • 왼쪽 자식 → 부모 → 오른쪽 자식
  • 이진 탐색 트리에서 정렬된 순서대로 값을 가져올 때 사용됨

후위 순회

  • 왼쪽 자식 → 오른쪽 자식 → 부모
  • 자식 노드부터 방문한다는 특성 때문에, 트리 삭제에 사용됨

이진 탐색 트리

  • 데이터가 작으면 왼쪽 자식으로, 크면 오른쪽 자식으로 구성된 트리

탐색 방법

  1. 찾으려는 값이 현재 노드의 값과 같으면 탐색을 종료
  2. 찾으려는 값이 현재 노드의 값보다 크다면 오른쪽 자식으로 탐색
  3. 찾으려는 값이 현재 노드의 값보다 작다면 왼쪽 자식으로 탐색
  4. 값을 찾으면 종료. 노드가 없을 때 까지 계속 탐색했는데 값이 없다면 트리에 값이 없는 것.

시간 복잡도

  • 기본적으로, 저장된 노드가 N개라면 시간 복잡도는 O(logN)임
  • 그러나 균형이 맞지 않을 때 (왼쪽/오른쪽 서브 트리의 높이 차가 1보다 큰 경우) 시간 복잡도는 배열 O(n)과 유사함

균형 이진 탐색 트리

  • 치우치지 않도록 균형을 맞춰 만들어 둔 트리
  • AVL 트리, 레드-블랙 트리 등 더 자세한 분류가 있음
  • 시간 복잡도를 O(logN)으로 유지함
  • 그러나 구현 난이도가 높음

그래프 뷰